DiffCSG: Differentiable CSG via Rasterization

Siggraph Asia 2024

Haocheng Yuan1, Adrien Bousseau2, Hao Pan3, Chengquan Zhang4, Niloy J. Mitra5,6, Changjian Li1
1University of Edinburgh, 2Inria, Université Côte d'Azur,
3Microsoft Research Asia, 4Nanjing University 5University College London, 6Adobe Research
Paper arXiv Video Code
Teaser Image

Given the CSG model of a bike (left), our DiffCSG renders the corresponding shape in a differentiable manner, such that its continuous parameters can be optimized to best match multi-view renderings of a target shape (right, pink). Our solution builds upon differentiable rasterization to compute image gradients with respect to CSG parameters (middle). Here we visualize the per-pixel gradient contribution for the global scale parameter 𝑠, the seat height ℎ, the handle size 𝑙, and the wheel radius 𝑟 (we cropped the gradient visualizations around the areas of interest for ℎ, 𝑙 and 𝑟). In this example, the optimization decreased the seat height, increased the wheel radius, and made the handles vanish by setting their size to 0 (top middle). The optimization also adjusted the orientation of the pedals.

Abstract

Differentiable rendering is a key ingredient for inverse rendering and machine learning, as it allows to optimize scene parameters (shape, materials, lighting) to best fit target images. Differentiable rendering requires that each scene parameter relates to pixel values through differentiable operations. While 3D mesh rendering algorithms have been implemented in a differentiable way, these algorithms do not directly extend to Constructive-Solid-Geometry~(CSG), a popular parametric representation of shapes, because the underlying boolean operations are typically performed with complex black-box mesh-processing libraries. 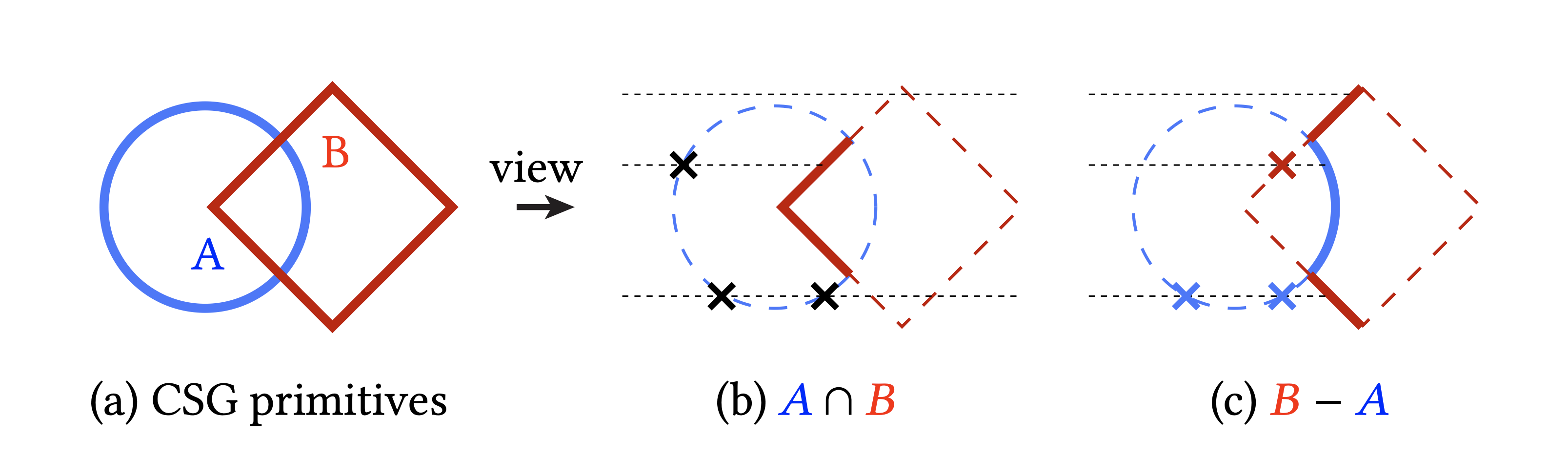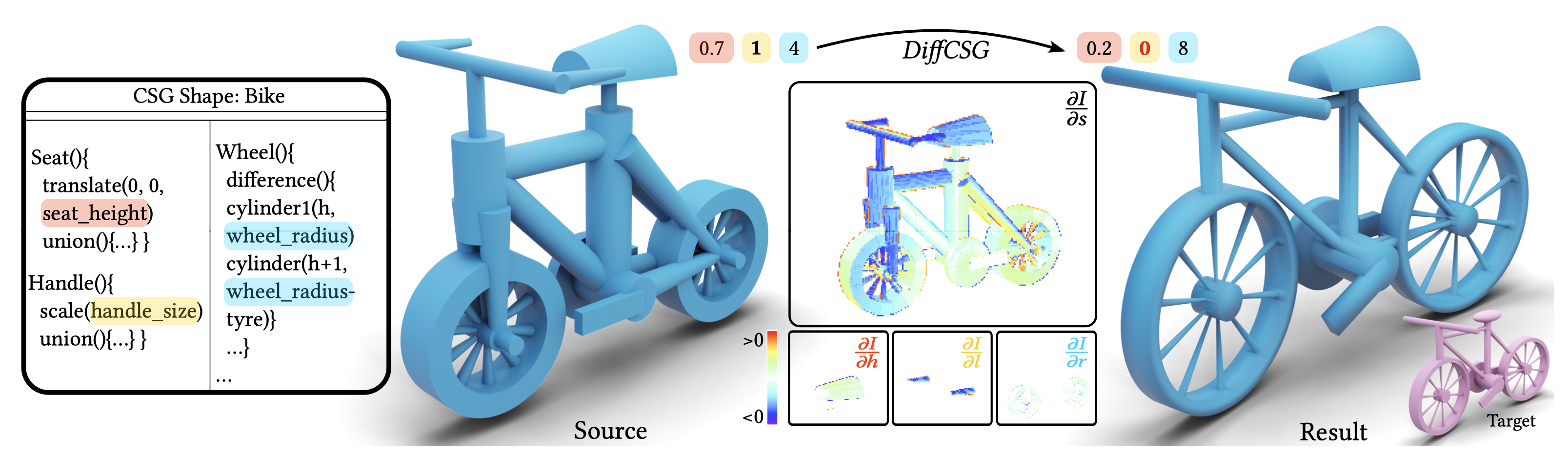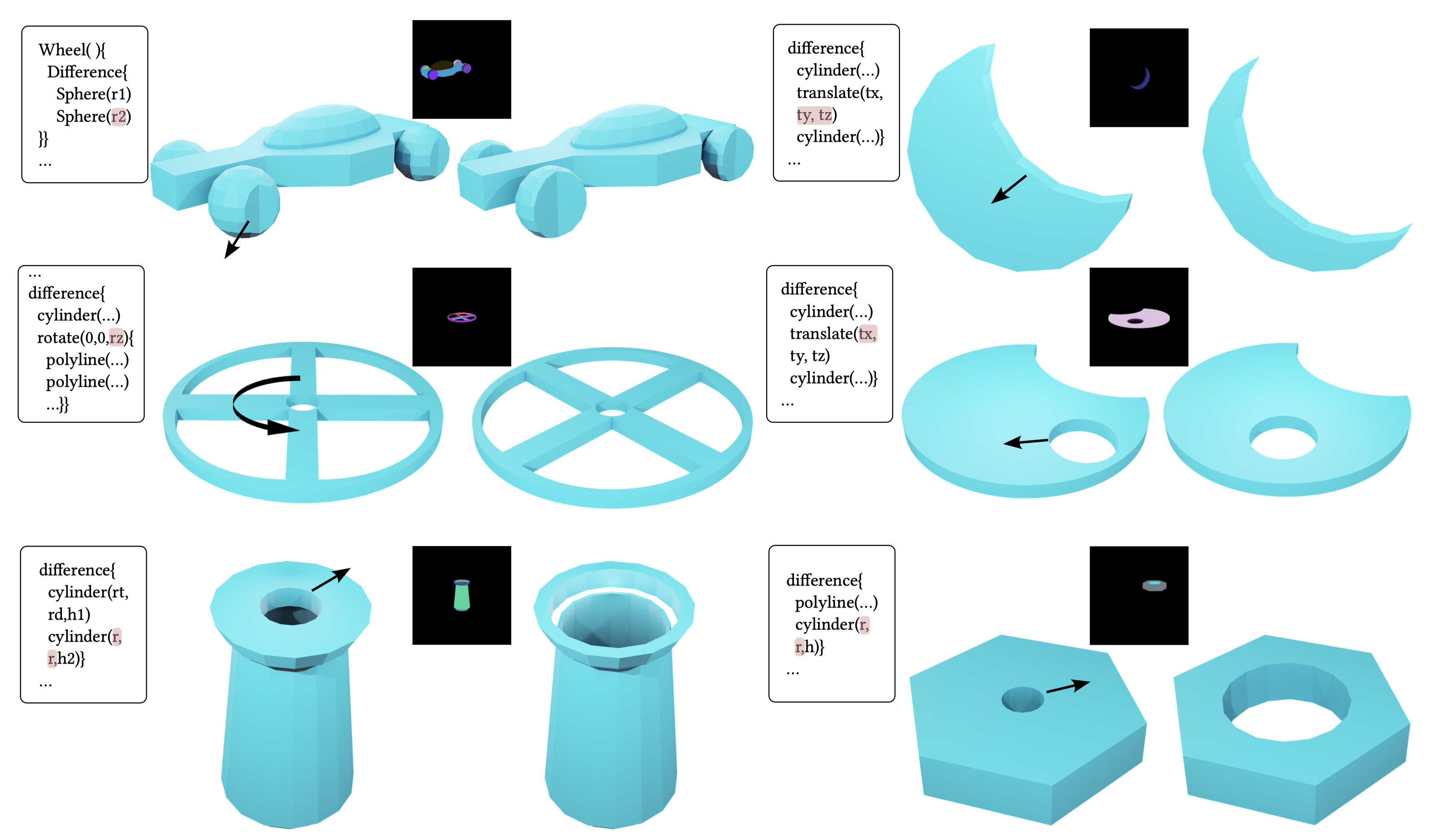We present an algorithm, DiffCSG, to render CSG models in a differentiable manner. Our algorithm builds upon CSG rasterization, which displays the result of boolean operations between primitives without explicitly computing the resulting mesh and, as such, bypasses black-box mesh processing. 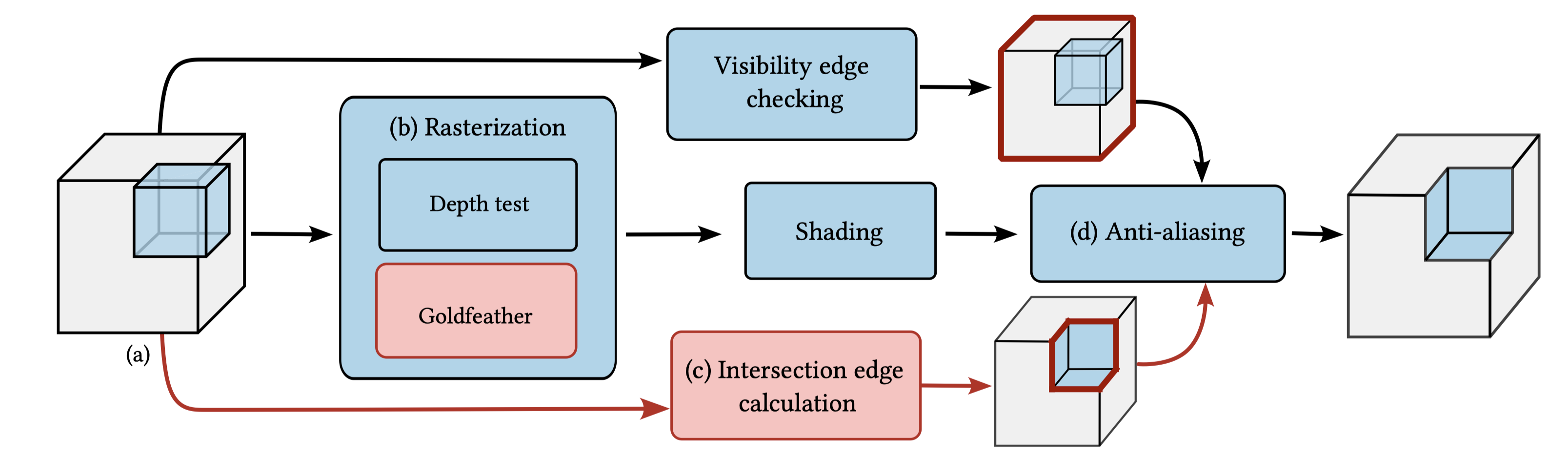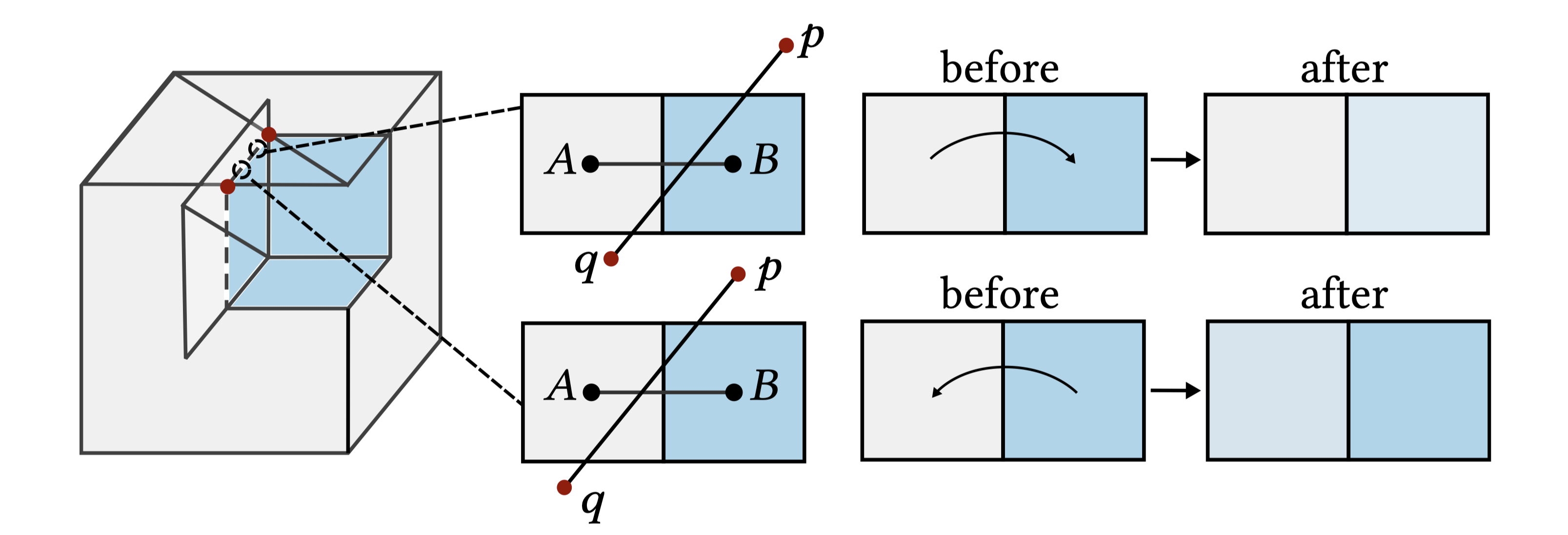We describe how to implement CSG rasterization within a differentiable rendering pipeline, taking special care to apply antialiasing along primitive intersections to obtain gradients in such critical areas. Our algorithm is simple and fast, can be easily incorporated into modern machine learning setups, and enables a range of applications for computer-aided design, including direct and image-based editing of CSG primitives.

Method

Method Image

Overview. Our algorithm adapts a differentiable rasterization pipeline (light blue) to render CSG models (a) in a differentiable way. First, we replace the standard depth test by the Goldfeather algorithm (b), which selects among front and back faces of the CSG primitives the ones to be displayed according to boolean operations. Second, we detect intersection edges between CSG primitives (c) and provide these edges to the anti-aliasing module (d). Proper anti-aliasing is critical to allow back-propagation of gradients from the final image all the way to the primitive parameters.

Goldfeather Algorithm

Processing Image

CSG Rasterization. The algorithm takes as input individual primitives of the CSG model (a). For an intersection, only the front-facing fragments that are occluded by an odd number of polygons are displayed (b, crosses depict occlusions along viewing rays). For a subtraction, the two primitives apply different parity tests against each other (c). Considering B - A, the algorithm displays the front-facing fragments of B that are occluded by an even number of polygons from A, and the back-facing fragments of A that are occluded by an odd number of polygons from B.

Antialiasing

Program Parsing

Pixel Antialiasing. On the left, an intersection edge (p,q) is formed by the top face of the gray cube and the vertical face of the blue cube. The two endpoints of the intersection edge are colored red.On the right, when considering the color blending of the crossing pixels (i.e., the gray pixel A and the blue pixel B) of the intersection edge, two typical options may apply depending on which pixel is most covered by the edge. In the top case, edge (p,q) intersects the segment connecting centers of A, B inside pixel B, which leads to the color of A blending into B, i.e. ColorBafter = α * ColorA + (1-α)* ColorBbefore. In the bottom case, the edge covers A the most, so the color of B is blended into A, i.e. ColorAafter = α * ColorB + (1-α) * ColorAbefore. The blending weight α is a linear function of the location of the crossing point, from zero at the midpoint to 0.5 at the pixel center. ß

Visual Result

Results Gallery

Visual Results. Examples of shapes from our benchmark that require proper treatment of intersection edges to be optimized. Without our anti-aliasing, the optimization remains stuck in its initial state due to the discontinuities introduced by the difference operator. In each example, the source shape, resultant shape, and one of the target images rendered with per-primitive colors are shown. Black arrows indicate the desired change between the source and the target.